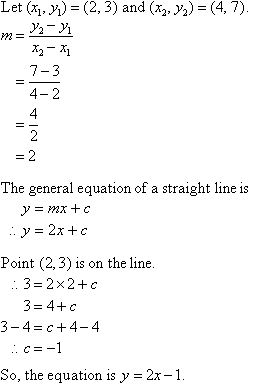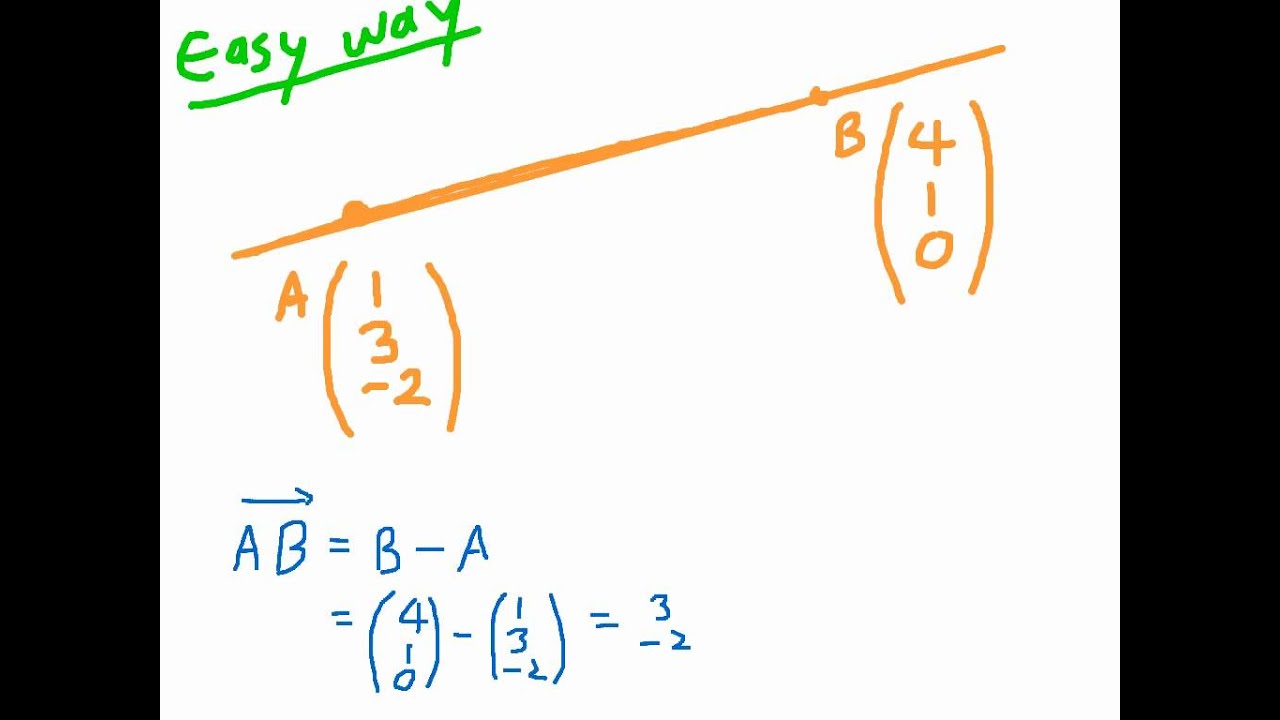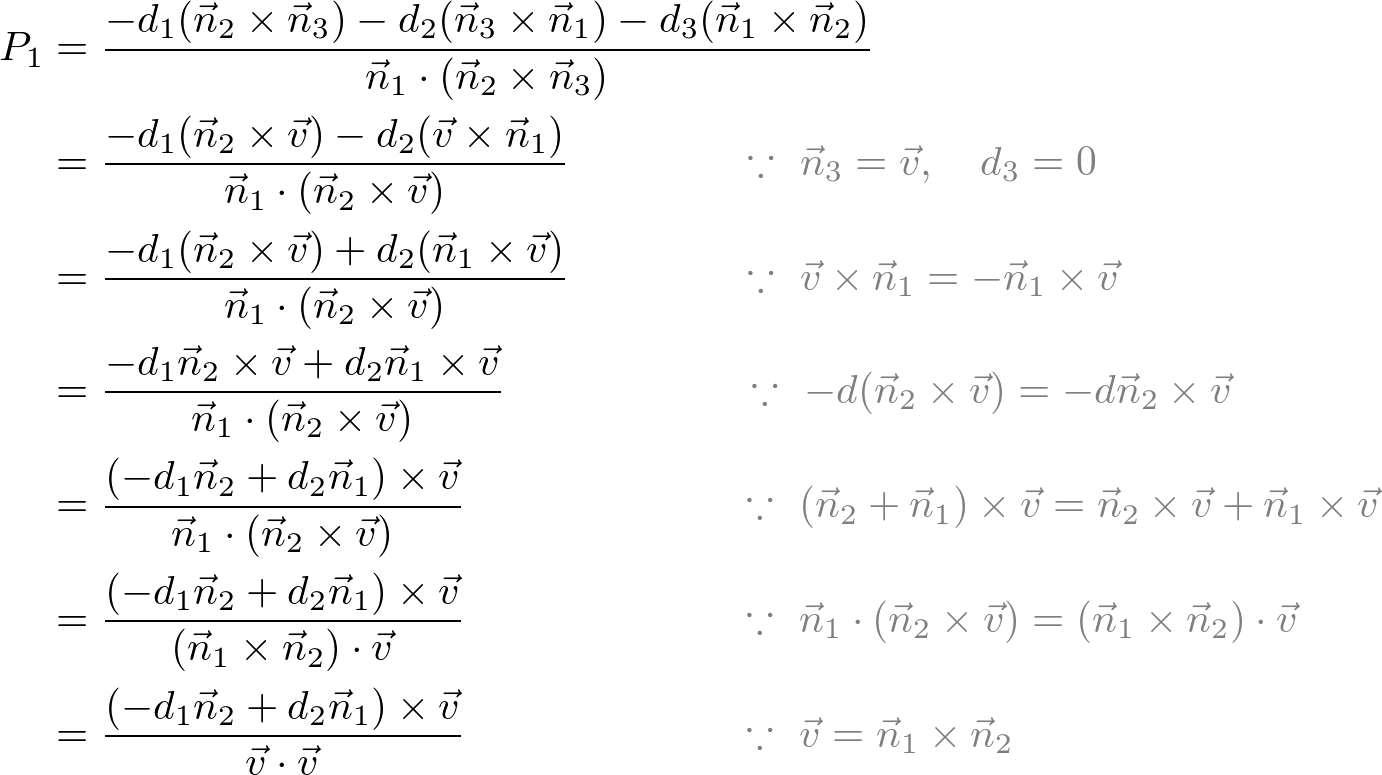Equation Of A Line In 3d With 2 Points

To give you an idea on how to derive it note that the expression.

Equation of a line in 3d with 2 points. Finding equation of a line in 3d. Y y2 y1 x2 x1 x x1y1. Thus x y z r 3. M change in ychange in x 4362 14.

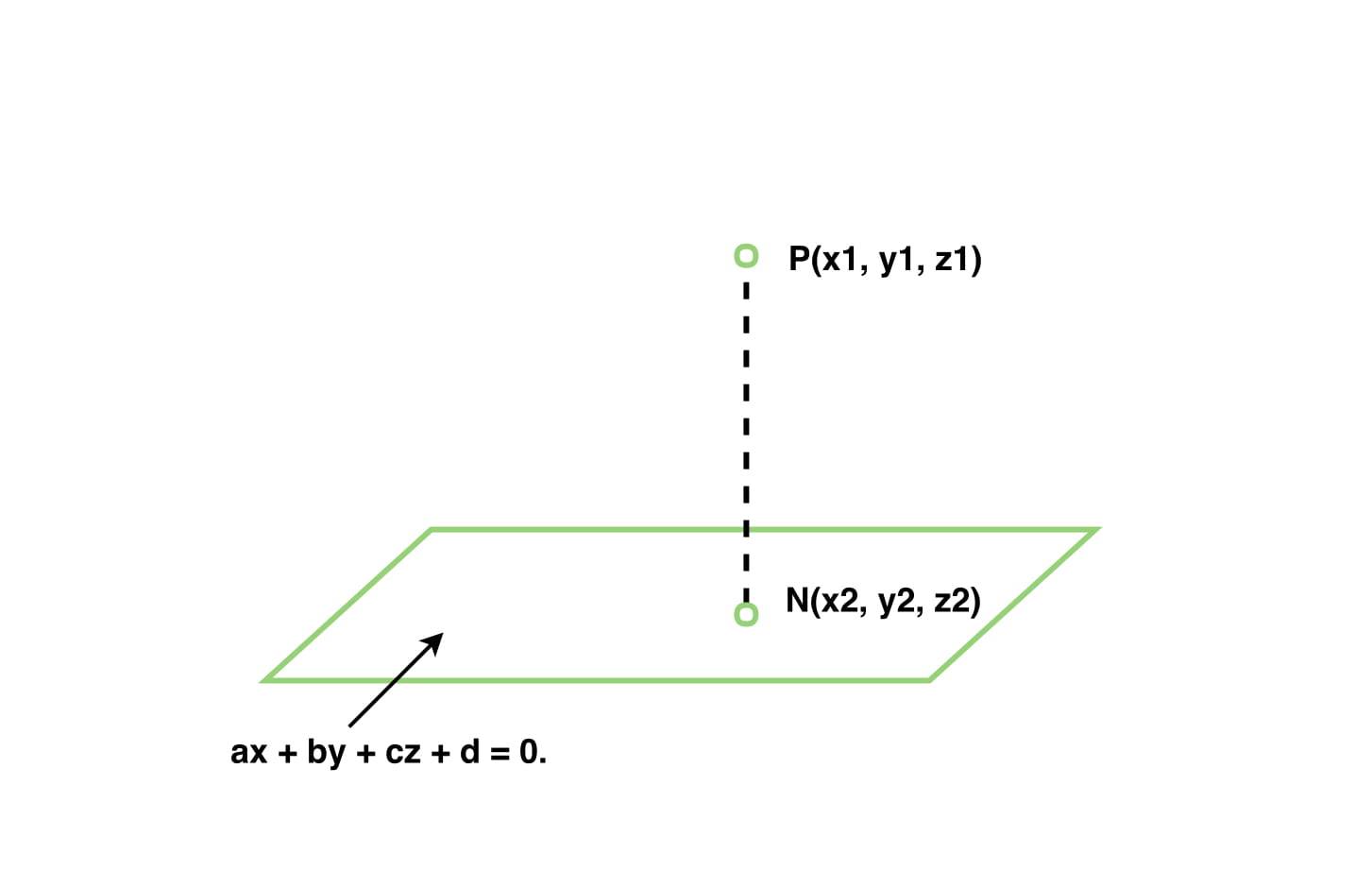
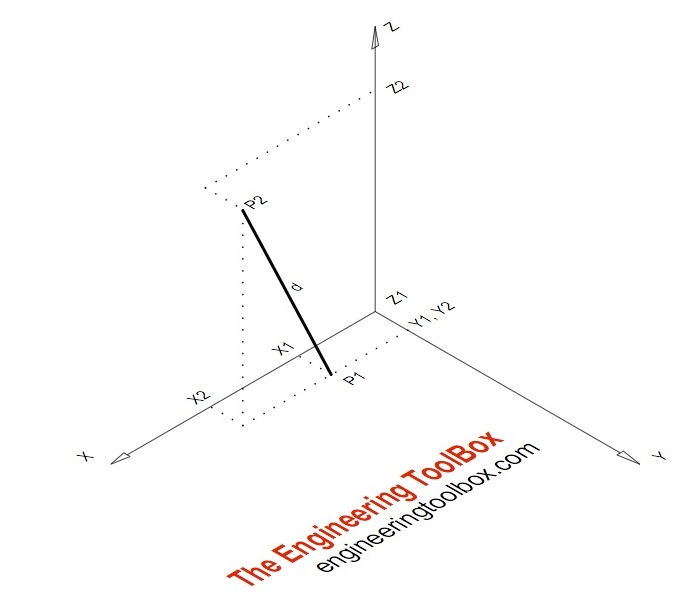
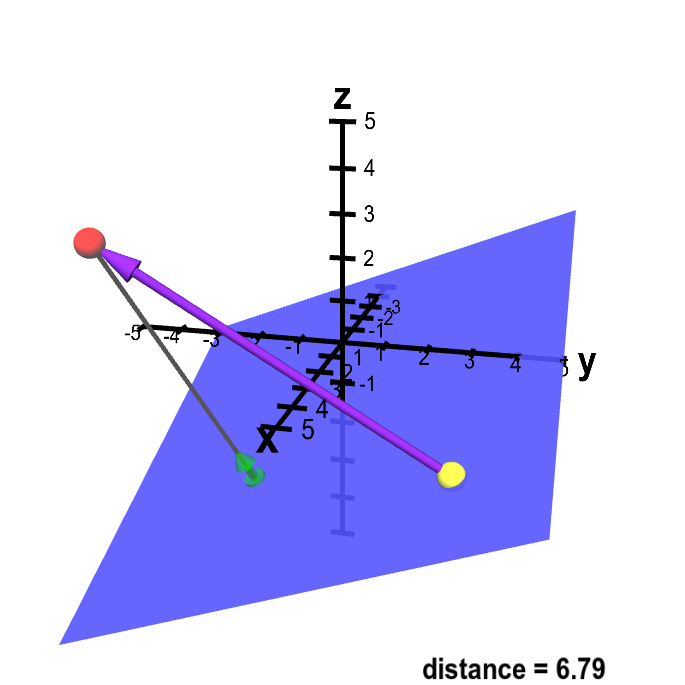
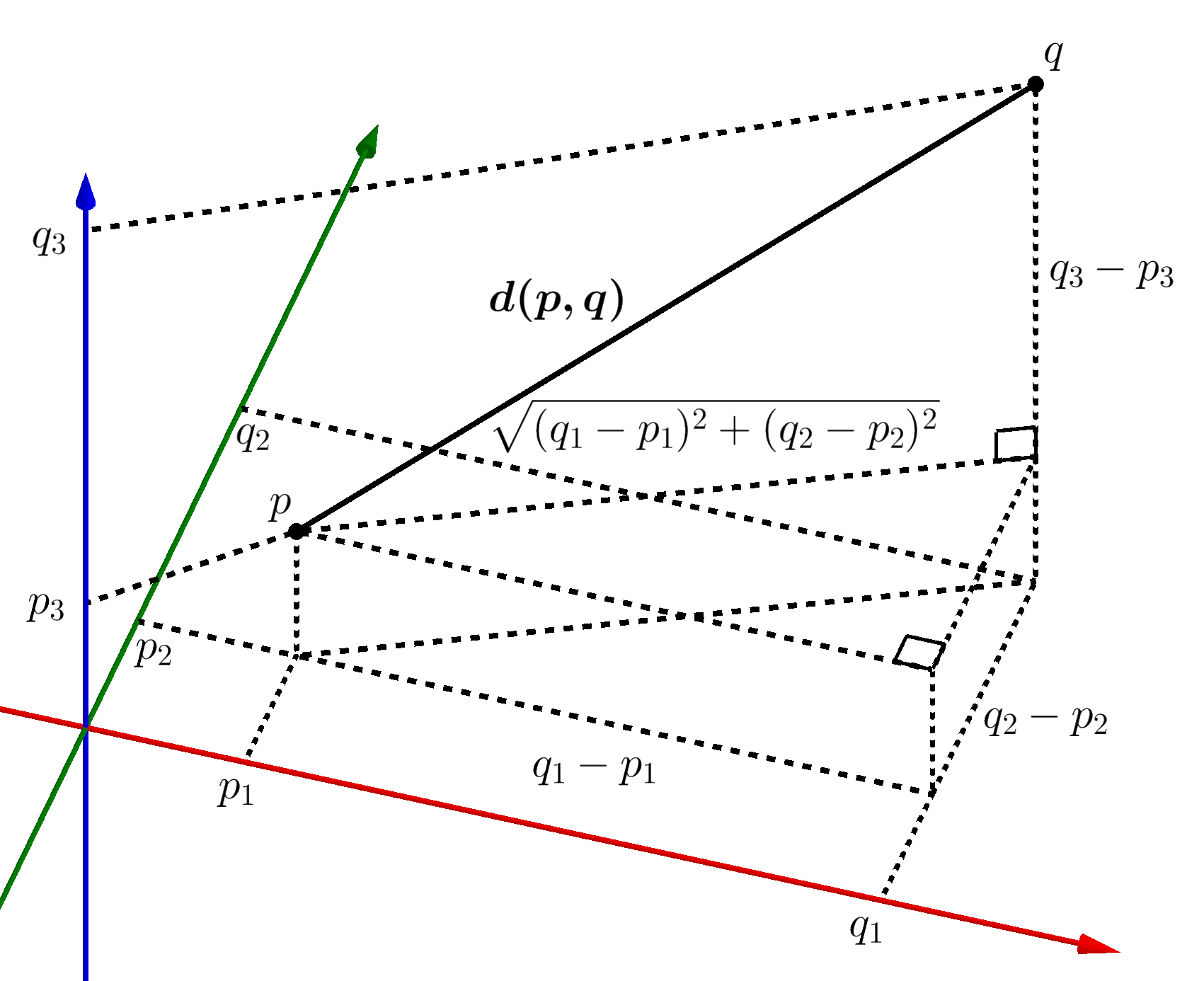
This answer is not useful. Show activity on this post. Y y 1 y 2 y 1 x 2 x 1 x x 1 and z z 1 z 2 z 1 x 2 x 1 x x 1 for planes you need three points. Subtracting the position vectors of the two points gives the direction vector which is.

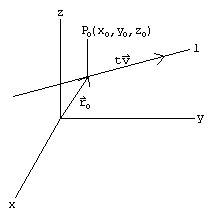
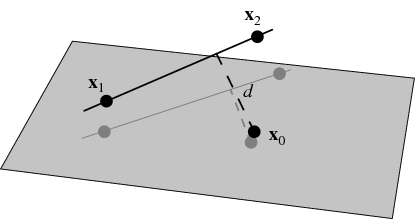
Line in 3d is determined by a point and a directional vector. This doesnt mean however that we cant write down an equation for a line in 3 d. D p q 2 0 2. For a line one can express it in parametric form.

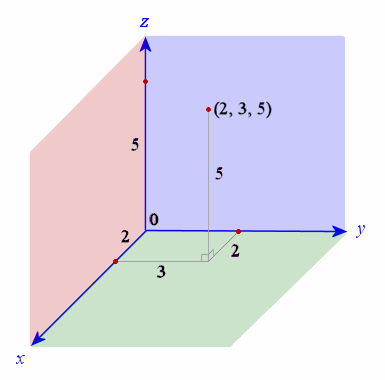
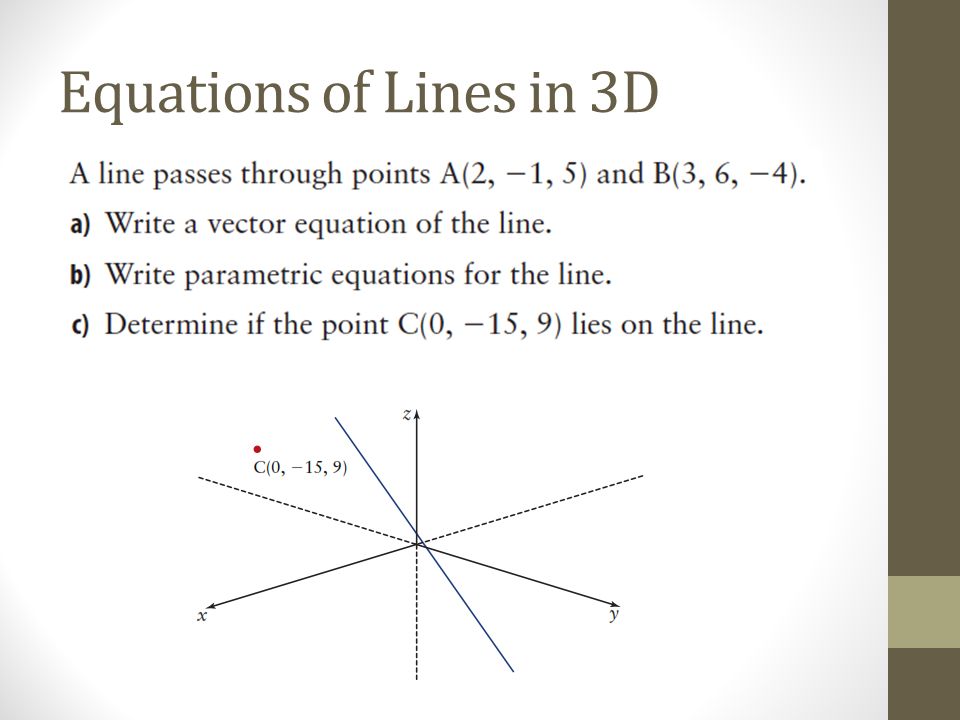
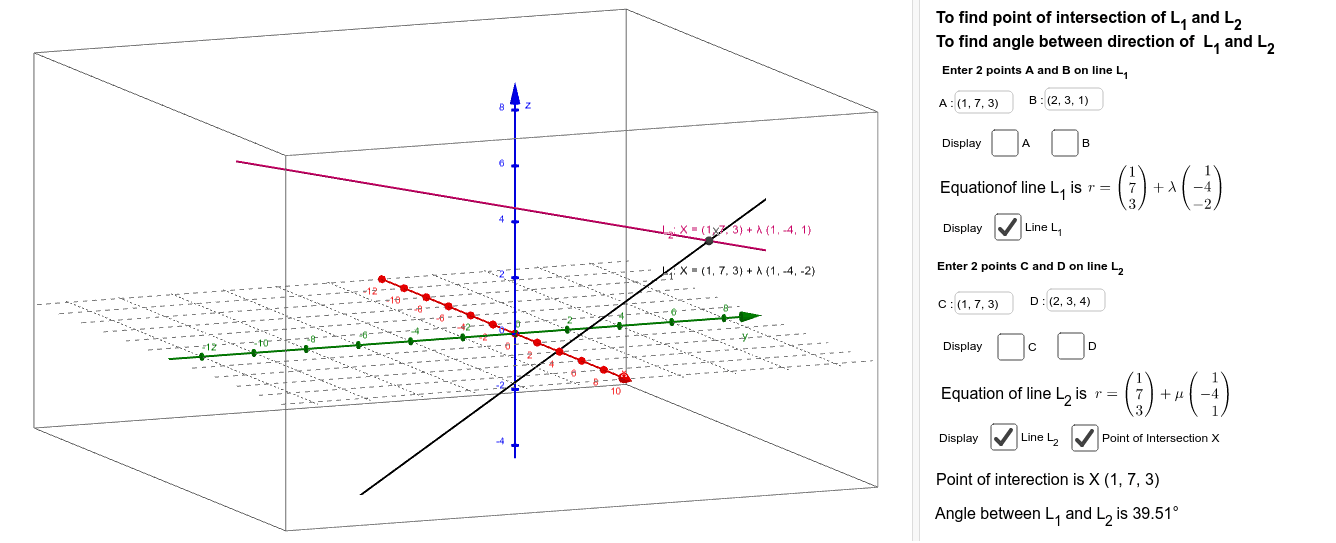
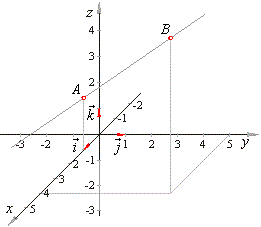
Vecr veca a vecb veca if the three dimensional coordinates of the points a and b are given as x 1 y 1 z 1 and x 2 y 2 z 2 then considering the rectangular coordinates of point r as x y z. From this we can get the parametric equations of the line. If we solve each of the parametric equations for t and then set them equal we will get symmetric equations of the line. Q 1 1 3.

This equation works except when x1x2 maybe there is a math wiz out there that knows of a work around but i am not a math wiz. For lines you need two equations so it is just duplicated. I was just trying to solve a problem. P 1 1 1 p 111 p 111 and.

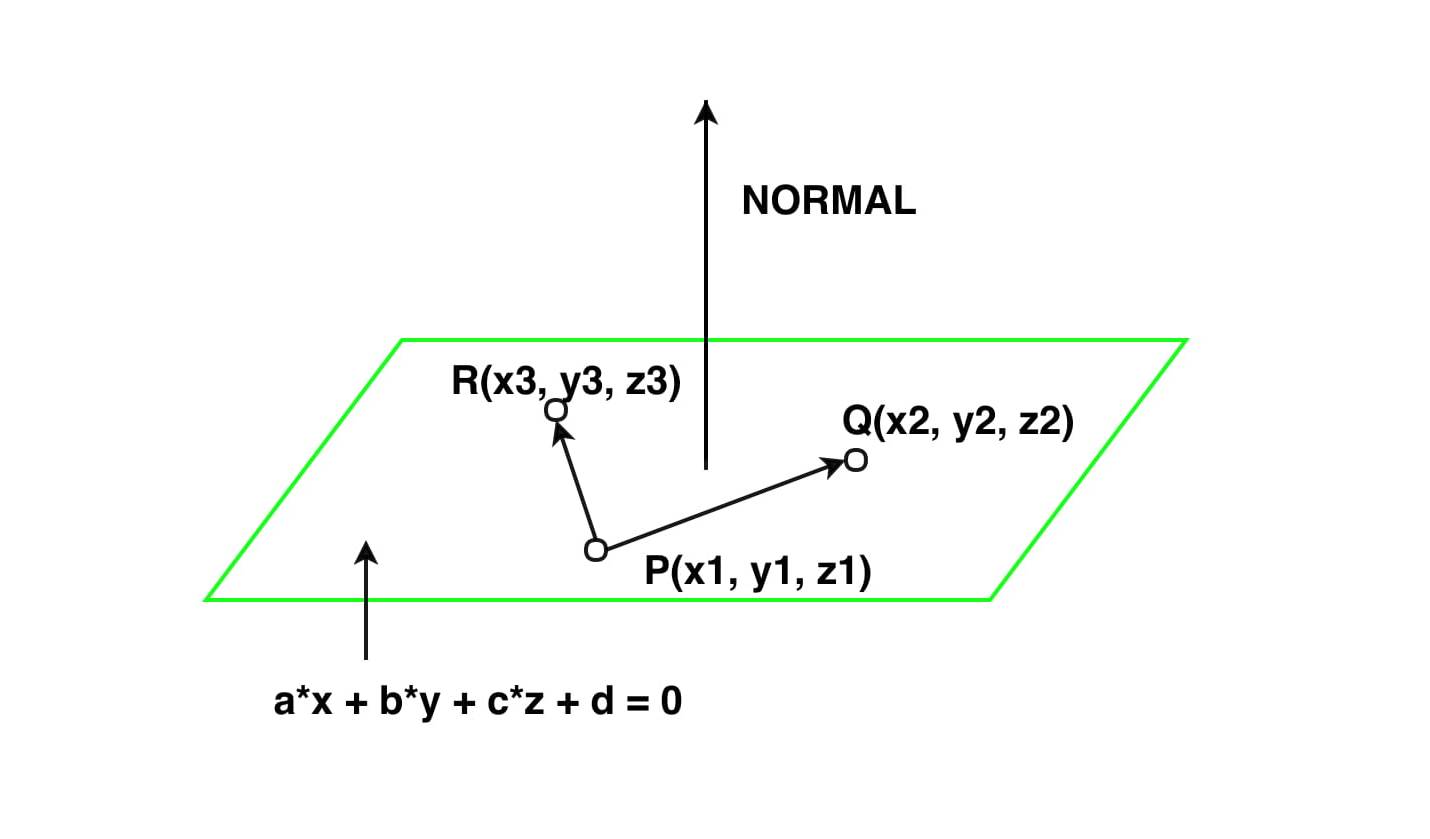
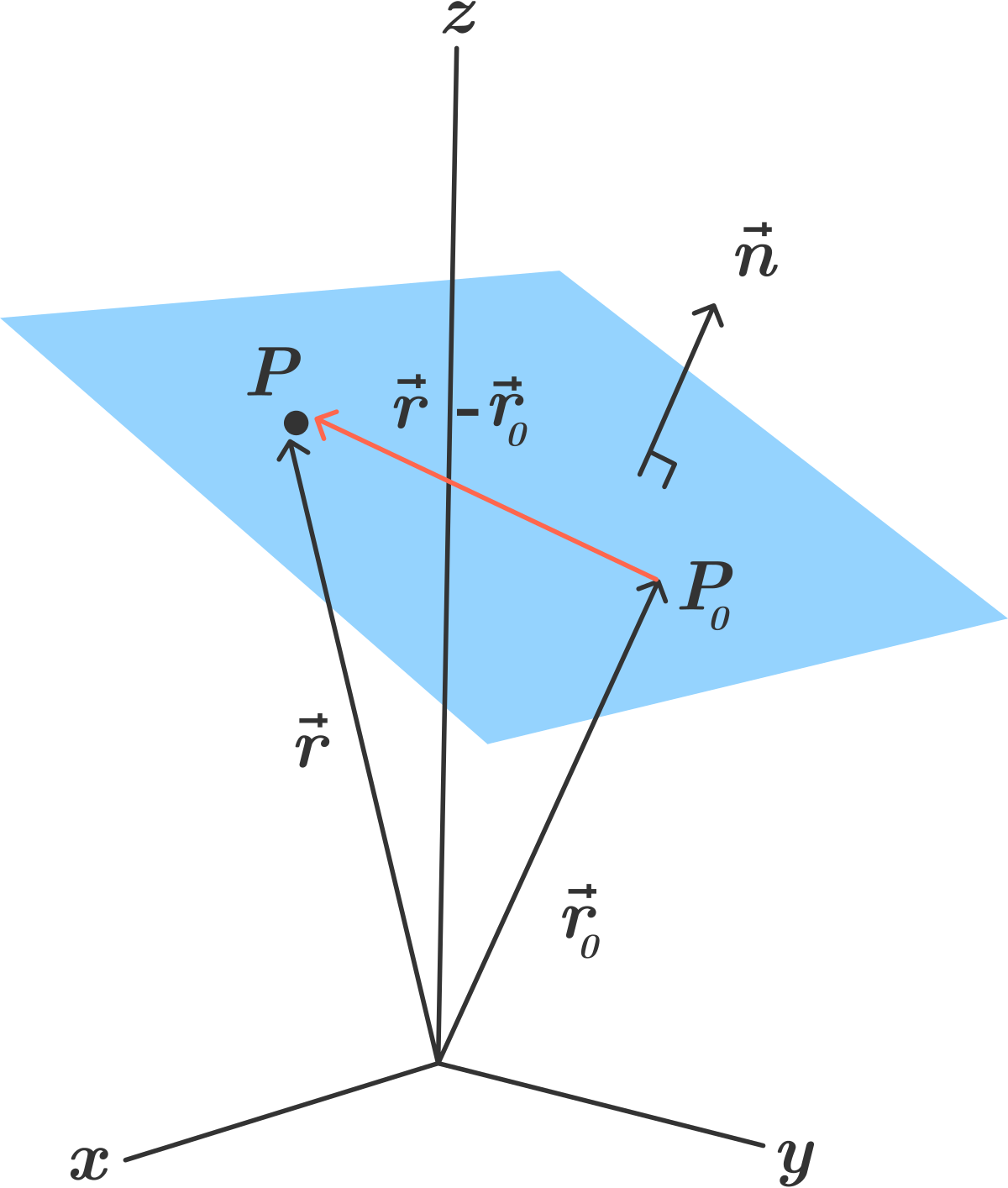
When x1x2 then the 3d line is confined to the plane perpendicular to the x axis which intersects the x axis at x1. P t p 0 d t. A 1 x b 1 y c 1 z d 1 and a 2 x b 2 y c 2 z d 2. You can describe a line in space as the intersection of two planes.

Y 3 mx 2 we already calculated the slope m. Alternatively you can use vector notation to describe it as. The directional vector can be found by subtracting coordinates of second point from the coordinates of first point. In this section we need to take a look at the equation of a line in mathbbr3.

Find the equation of the line that passes through the two points. Y y 1 mx x 1 we can choose any point on the line for x 1 and y 1 so lets just use point 23. Start with the point slope formula x 1 and y 1 are the coordinates of a point on the line. Vec dvec pq 202.